Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

[ 1 ] 2 3 4 ... 27

Инженерные конструкции можно рассматривать как некоторую совокупность конструктивных элементов, соединенных в конечном числе узловых точек. Если известны соотношении между силами и деремещениями для каждого отдельного элемента, то, используя хорошо известные приемы строительной механики [I-5], можно описать свойства и исследовать поведение конструкции в целом.

В сплошной среде число точек связи бесконечно, и именно это составляет основную трудность получения численных решений в теории упругости. Понятие конечных элементов, введенное впервые Тернером и др. [6], представляет собой попытку преодолеть эту трудность путем разбиения сплошного тела на Отдельные элементы, взаимодействующие между собой только в узловых точках, в которых вводятся фиктивные силы, эквивалентные поверхностным напряжениям, распределеннйм по границам элементов. Если такая идеализация допустима, то задача; сводится к обычной задаче строительной механики, которая может быть решена численно.

На первый взгляд, этот иитуитив-но понятный и доступный инженерный метод выглядит не совсем убедительно - в частности, остается открытым вопрос о соотношениях между силами и перемещениями отдельных элементов. Способы получения этих соотношений будут подробно рассмотрены в гл. 2 после изложения основ метода. На данном же этапе целесообразно кратко описать общий метод расчета конструкций, который будет широко использоваться в книге после рассмотрения свойств конечных элементов.

В дальнейшем будет показано, что метод конечных элементов применим и ко многим задачам иного типа, но и тогда основные свойства элемента выражаются в форме, принятой в строительной механике. Общие методы составления ансамбля и решения задач аналогичны приемам строительной механики.

В действительности структурная форма уравнений присуща не только строительной механике. Уравнения в такой

ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ: МЕТОД ЖЕСТКОСТЕИ РАСЧЕТА КОНСТРУКЦИИ И ИССЛЕДОВАНИЕ СЕТЕЙ

форме используются при расчетах электрических цепей или потоков жидкости в трубопроводах. Подобные задачи часто называются задачами исследования сетей').

1.2. Элемент конструкции

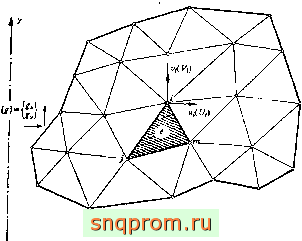
На фиг. 1.1 изображена двумерная конструкция, состоящая из отдельных частей, соединенных между собой в точках, пронумерованных от 1 до п. Соединения в узлах предполагаются шарнирными.

Сначала допустим, что в результате расчета или па основе экспериментальных данных достоверно известны характери-

р

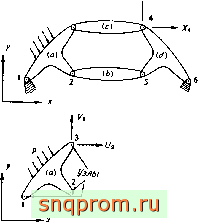
Типичный элетент Фнг. 1.1. Типичная конструкция, составленная из отде.тьных элементов.

стики каждого элемента. Силы, возникающие в узлах 1-3 элемента а, однозначно определяются перемещениями этих узлов, действующей на элемент распределенной нагрузкой р и его начальной деформацией. Начальная деформация может быть обусловлена температурным воздействием, усадкой или несо- вершенством сборки. Силы и соответствующие им перемещения определяются компонентами (/, V и и, о в какой-либо системе координат.

). Вместо понятия сети в литературе все чаще используется более общее понятие графа. - Прим. ред.

Записывая силы, действующие во всех (в трех для рассматриваемого случая) узлах элемента а, в виде матрицы'), получим

{рг=-

(1.1)

а для соответствующих перемещений узлов

(1.2)

Если предположить, что элемент упругий, то основные соотношения всегда могут быть записаны в виде

{fr=[&r{6r-b{f};+{f}:, (1.3)

где {Р}р~ силы, уравновешивающие действующие на элемент распределенные нагрузки, {F},- силы в узлах, обусловленные начальными деформациями, которые м.огут возникать, например, при изменении температуры без перемещения узлов. Первый член в этой формуле представляет собой силы, вызванные перемещениями узлов.

Предварительный расчет или эксперимент позволяет однозначно определить напряжения в любой заданной точке через узловые перемещения. Записывая эти напряжения в виде матрицы {а} , получаем соотношение в форме

{аГ = [5Г{бГ-Ь{а};-Ь{а}:.

(1.4)

где последние два члена - напряжения, обусловленные распределенными нагрузками, и начальные напряжения при отсутствии узловых перемещений.

) Для понимания материала, изложенного в книге, требуется знание основ матричной алгебры. Это необходимо для краткости и удобства изложения. Для читателей, не знакомых с матричной алгеброй, необходимые сведения приведены в небольшом по объему приложении 1,

Матрица {kY называется матрицей жесткости элемента, а [S] - матрицей напряжения элемента.

Соотношения (13) и (1.4) проиллюстрированы на примере элемента стремя узлами, в каждом из которых действуют только две компоненты силы. Ясно, что все рассуждения и определения справедливы и в более общем случае. Элемент b в рассматриваемом случае связан с соседними только в двух точках, хотя другие элементы могут иметь таких точек и больше. С другой стороны, - если соединения элементов считать жесткими, то требуется рассматривать по три компоненты обобщенной силы и обобщенного перемещения, причем за третьи компоненты следует принять соответственно момент вращения и угол поворота. Для жесткого соединения в трехмерной конструкции число компонент в узле равняется шести. Таким образом, в общем случае

(1.5)

где Р{ и б,- имеют одинаковое число компонент или степеней свободы.

Ясно, что матрицы жесткости элемента всегда будут квадратными вида

		и {6} =

(1.6)

где kii и t. д. - также квадратные подматрицы размерности / X а I - число компонент силы в рассматриваемых узлах.

В качестве примера рассмотрим двумерную задачу о шар-нирно опертой балке постоянного сечения А с модулем упругости Е (фиг, 1.2). Балка нагружена равномерно распределенной поперечной нагрузкой р н подвержена однородной температурной деформации

8о = аГ.

Если концы балки имеют координаты д:,-, (/< и Хп, Уп, то ее длина может быть вычислена как

L = <s/{{x -Xif+iy,-yif}, а ее угол наклона к горизонтальной оси

В каждой узловой точке необходимо рассмотреть только по две компоненты силы и перемещения.

Очевидно, что узловые силы, обусловленные пдперечной нагрузкой, записываются в виде матрицы

Ui\ -sina> Vi cos a

(/ - sin a

V )p V cos a J

\pL

Элементы этой матрицы равны соответствующим компонентам реакций опор балки, т. е. рЦ2. Для компенсации температур-

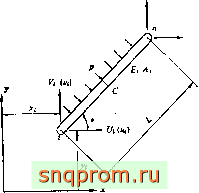
Фиг. 1.2. Шарнирио опертая балка.

ного расширения ео нужно приложить осевую силу ЕаТА, компоненты которой

Ut-\ - cos а

- sin а cos а sin а

Наконец, перемещения узловых точек элемента

{ЕаТА).

вызовут его удлинение (и„ -Uj)cosa + (t) --t;<)sma. Величина удлинения, умноженная иа EAjL, даст осевую силу, компоненты которой можно найти, подставив величину этой силы вместо -ЕаТА в предыдущее выражение. Стандартная форма записи имеет вид

Ui Vi

Sin a COS a

sinacosa sina

- cos a - sin a cos a

- cos a - sin a cos a -sinacosa -sina

- sin a cos о

cos a sin a cos a

- sin a

sinacosa sin a

Итак, для рассматриваемого простейшего случая определены все слагаемые основного уравнения (1.3). Нетрудно записать в форме (1,4) и напряжения в любом поперечном сечеиии элемента. Если, например, ограничиться рассмотрением среднего сечения балки С, то напряжения, возникающие в результате осевого растяжения и изгиба элемента, можно записать в виде

02 J с . -

- COS а - sma cos а - sin а

cos а sin а COS а sin а.

где d-половина высоты сечения, а / - момент инерции. Легко заметить, что в это выражение входят все слагаемые формулы (1.4).

Для более сложных элементов требуются более тонкие приемы расчета, но все равно результаты имеют такую же форму. Инженер легко заметит, что зависимость между наклоном и прогибом, используемая при расчетах жестких р^ам, является частным случаем рассмотренных общих соотношений.

Следует отметить, что полная матрица жесткости для деформируемого элемента получилась симметричной (то же можно

сказать и о подматрицах). Это никоим образом не случайно, а вытекает из закона сохранения энергии и его следствия - теоремы взаимности Максвелла - Бетти.

Во всех рассуждениях предполагалось, что свойства элемента описываются простыми линейными соотношениями. В принципе можно было бы получить аналогичные соотношения и для нелинейных материалов, однако обсуждение задач такого рода выходит за рамки этой монографии.

1.3. Составление ансамбля и расчет конструкции

Рассмотрим снова гипотетическую конструкцию, изображенную на фиг. 1.1. Чтобы получить решение, нужно удовлетворить

а) условиям совместности и

б) уравнениям равновесия.

Любая система {6} узловых перемещений

{б} =

(1.7)

записанная для конструкции, в которую входят все элементы, автоматически удовлетворяет первому условию.

Поскольку условия равновесия внутри каждого элемента считаются выполненными, необходимо удовлетворить условиям равновесия в узловых точках. Полученные уравнения будут содержать в качестве неизвестных перемещения. Как только они будут найдены, задачу расчета конструкции можно считать решенной. Внутренние усилия (напряжения) в элементе могут быть легко определены с помощью зависимостей, априори установленных для каждого элемента в виде (1.4).

Предположим, что, помимо распределенной нагрузки, приложенной к каждому отдельному элементу, конструкция нагружена внешними силами

{R} =

(1.8)

приложенными в узловых точках. Каждая из сил /?( должна иметь столько же компонент, сколько и рассматриваемые реакции элемента. В обсуждаемом примере

(1.9)

так как соединения предполагались шарнирными. Однако в общем случае будет рассматриваться произвольное число компонент.

Если теперь нужно удовлетворить условиям равновесия в произвольной узловой точке г, то каждая из компонент Rt должна быть приравнена сумме компонент сил от всех элементов, соединяющихся в этом узле. Таким образом, рассматривая все компоненты силы, получаем

{Ri} = I,{Fir = {Fiy+{F,r+ .... (1.10)

где Fi - сила, приложенная к узлу со стороны элемента 1, Р] - сила, приложенная к узлу со стороны элемента 2, и т. д. Очевидно, что отличные от нуля силы будут давать только элементы, содержащие точку i, однако суммирование проводится по всем элементам.

Подставляя (1.3), получаем выражения для сил в узловой точке 1

{Ri} = (Е \киГ) {6,} -Ь (Е \ki,r) {ь,} + ...

+E{};+E{fj;. (1.11)

и здесь вклад в сумму дают только элементы, соединяющиеся в узле i. Объединяя все такие уравнения, имеем

(1.12)

где подматрицы

[K]{6}=.{/?}-{f}-{fK,

[*Г,.1=Е1*<тГ,

{/Лр=Е№}?. {Л},=Е{Л}:

(1.13)

получены суммированием по всем элементам. Это простое правило составления ансамбля очень удобно, поскольку сразу после определения коэффициента для отдельного элемента он может быть немедленно заслан в соответствующую ячейку памяти вычислительной машины. Составление ансамбля является основной операцией метода конечных элементов, и поэтому она должна быть хорошо усвоена читателем.

Если используются разные типы элементов, то при составлении ансамбля следует помнить, что можно складывать матрицы только одинаковой размерности. Следовательно, отдельные подматрицы, которые включаются в систему, должны содержать одинаковое число компонент сил и перемещений. Так, например, если к какому-либо элементу конструкции в узловой точке, передающей моменты, присоединен шарнирно другой элемент, то

матрицу жесткости последнего необходимо дополнить, вводя соответствующие (нулевые) значения на места углов поворота или моментов.

Систему уравнений (1.12) можно решить, как только будут подставлены перемещения опор. В примере (фиг. 1.1), где обе компоненты перемещений узлов 1 и 6 равны нулю, это будет означать подстановку

что эквивалентно уменьшению числа уравнений равновесия (в рассматриваемом случае их двенадцать) и вычеркиванию первой и последней строки и столбца. Таким образом, общее число неизвестных компонент перемещения уменьшается до восьми. Тем не менее всегда удобно составлять уравнения в соответствии с соотношением (1.12), учитывая вбе узловые точки.

Очевидно, что эту систему невозможно решить без задания некоторого числа перемещений, исключающих смещение конструкции как жесткого целого, так как по заданным силам нельзя однозначно определить перемещения. Этот физически очевидный факт математически выражается тем, что матрица \К\ является сингулярной, т. е. не имеет обратной. Задание соответствующих перемещений по окончании формирования ансамбля обеспечивает возможность получения единственного решения путем вычеркивания соответствующих строк и столбцов различных матриц.

Несмотря на то что подстановка известных перемещений, позволяющая уменьшить общее число решаемых уравнений, является относительно простой операцией при ручных вычислениях и может быть запрограммирована для вычислительных машин, часто оказывается удобным непосредственно решать первоначальную систему уравнений с тем, чтобы избежать реорганизации машинной памяти. Это осуществляется очень просто с помощью искусственного приема, предложенного Пейном и Айронсом [7].

При использовании такого приема вместо исключения уравнения равновесия, в котором некоторое перемещение считается заданным (а соответствующая компонента внешней силы остается неизвестной), и последующей подстановки этого перемещения в остальные уравнения диагональный элемент матрицы [К\ в рассматриваемой точке умножается на очень большое число. Одновременно член, стоящий в правой части уравнения, заменяется тем же самым числом, умноженным на заданное значение перемещения. В результате уравнение заменяется другим, но величина перемещения в рассматриваемом случае равна определенному значению. При этом общее число уравнений в

системе остается неизменным. Подробно этот вопрос обсуждается в гл. 20.

После определения неизвестных перемещений легко вычислить напряжения и внутренние силы, применяя соотношение (1.4) поочередно к каждому элементу.

1.4. Преобразование координат

Часто бывает удобно определять характеристики отдельного элемента в системе координат, отличной от той, в которой задаются внешние силы и перемещения конструкции в целом. Чтобы облегчить вычисления, для каждого элемента можно использовать свою систему координат. Компоненты сил и перемещений, входящие в соотношение (1.3), нетрудно записать в любой системе координат. Очевидно, что это необходимо сделать до составления ансамбля.

Систему локальных координат, в которой определены характеристики элемента, будем помечать штрихом, чтобы отличить ее от системы координат, принятой для описания конструкции в целом. Компоненты перемещений преобразуются с помощью матрицы направляющих косинусов [L]:

{6Г = 11]{6Г. (1.14)

Так как в любой системе координат соответствующие компоненты сил должны совершать одинаковую работу), то

{{Р}Г{ьг=({РГ)ЧьГ,

и, используя формулу (1.14), получаем

({Р}Г{6Г==({Р'}Г[Ц{ЬГ

или

{pr = [LY{pr. (1.15)

Преобразования, определяемые соотношениями (1.14) и (1.15), называются контрграднентными.

Чтобы преобразовать жесткости, определенные в локальной системе координат, к глобальным координатам, отметим, что

{ру = [k] {б'}

и в силу (1.14) и (1.15)

\kr = [LY[kr[L].

(1.16)

(1.17)

)() означает транспонирование матрицы ( ).

Читатель может убедиться в полезности вышеуказанных преобразований, применив их для рассмотренного шарнирно опертого стержня. В более сложных задачах для некоторых типов внешних связей, описываемых соотношениями вида (1.14),i числа' степеней свободы {6} и {S} могут быть различными. Однако и в этих случаях соотношения (1.15) и (1.16) остаются справедливыми.

1.5. Электрические и гидравлические сети

Аналогичные принципы получения характеристик элемента и ансамбля могут быть использованы во многих различных областях, не связанных с расчетом конструкций. Для примера рас-

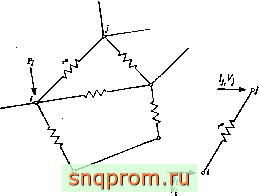
Фиг. 1.3. Цепь электрических сопротивлений.

смотрим цепь электрических сопротивлений, изображенную иа фиг. 1.3.

Если типичный элемент - сопротивление (/ - рассмотреть изолированно от системы, то с помощью закона Ома можно записать соотношение между входящими токами и напряжениями на его концах:

или в матричном виде

	j 1	- 1	-1

что в принятой нами стандартной форме выглядит как

{ir = [kY{vr. (1.18)

Ясно, что в такой форме это соотношение соответствует (1.3). Действительно, если бы к элементу извне подводился ток, то можно было бы найти величины усилий в элементе.

Для составления ансамбля следует сделать предположение о непрерывности потенциала в узловых точках и учесть баланс токов. Если теперь Pi обозначает внешний входящий ток в точке i, то придем к уравнению, аналогичному (1.11):

=EELVm. (1.19)

Второе суммирование проводится здесь по всем элементам. Для всей совокупности узлов имеем

{P} = [K]{V}, (1.20)

где

kij = Е z-

Здесь скобки опущены, так как такие величины, как напряжение и ток, а следовательно, и коэффициенты матрицы жесткости являются скалярными величинами.

Если вместо сопротивлений рассмотреть ламинарное течение жидкости в трубах, то опять можно получить то же уравнение, но V будет представлять собой гидравлический напор, а / - расход жидкости.

. Для встречающихся на практике систем трубопроводов линейные законы, вообще говоря, несправедливы. Как правило, соотношение между напором и расходом имеет вид

li=c(Vi-V,)\ (1.21)

где показатель у изменяется в пределах между. 0,5 и 0,7. Но и в этом случае основные соотношения можно записать в форме (1.18) с той лишь разницей, что матрицы представляют собой уже не массивы констант, а известные функции от {V}. Эти уравнения можно объединить для всего ансамбля, но они уже будут нелинейными. В общем случае их можно решить одним из итерационных методов.

Наконец, упомянем о более общей форме электрической цепи переменного тока. Зависимости между током и напряжением для таких цепей обычно записываются в комплексной форме, причем сопротивление заменяется комплексным сопротивлением. Таким образом, опять будут получены соотношения в стандартной форме (1.18) -(1.20), причем каждая величина будет иметь прйствительную и мнимую части.

При решении такого рода задач можно использовать обычные методы, рассматривая каждое соотношение отдельно для действительных и мнимых частей. Кроме того, современные цифровые вычислительные машины позволяют использовать стандартные приемы программирования операций с комплексными числами. В одной из последующих глав, посвященной вопросам колебаний, мы коснемся некоторых задач этого класса.

1.6. Общая схема исследования

Для того чтобы читатель мог лучше разобраться в изложенном материале, рассмотргм следующий пример. На фиг. 1.4, а

г

а 3

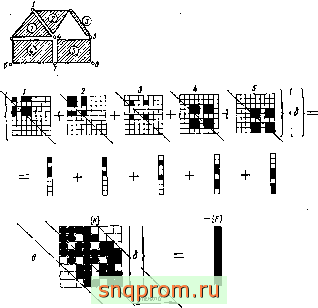
Фиг. 1.4 Пример.

изображено пять взаимосвязанных элементов. Это могут быть элементы конструкции, электрической цепи или элементы любого другого линейного типа. Решение задачи состоит из нескольких этапов,

Первый этап заключается в определении свойств элемента на основании исходных данных о его геометрии, материале н нагрузке. Для каждого элемента матрица жесткости и соответствующие узловые силы находятся в виде (1.3). Каждый элемент имеет свой собственный номер и узловые точки.

Например, элемент 1 связан с другими в узлах 1, 3, 4, элемент 2 -в узлах 1, 4, 2, элемент 3 - в узлах 2, 5, элемент 4 - в узлах 3, 4, б, 7, элемент 5 - в узлах 4, 7, 8, 5. Определяя характеристики элемента в глобальных координатах, мы можем ввести каждую компоненту жесткости или силы на соответствующее место в глобальной матрице, как это показано на фнг. 1,4,6. Каждый зачерненный квадрат соответствует одному коэффициенту или подматрице типа [ki,] (если рассматривается более одной компоненты силы). Здесь же показан вклад каждого элемента, и читатель может проверить правильность расположения коэффициентов. Заметим, что использование различных типов элементов не создает дополнительных трудностей. (Для простоты все силы, включая узловые, отнесены к соответствующим элементам.)

Второй этап - это составление полной системы уравнений типа (1.12). Она получается непосредственно путем использования соотношений (1.13) н простого суммирования всех составляющих по элементам в глобальной матрице. Результат показан на фиг. 1.4, в, где места расположения ненулевых коэффициентов зачернены.

В силу симметрии матрицы достаточно определить только элементы, расположенные на главной диагонали и над ней.

Все ненулевые коэффициенты расположены внутри ленты, ширина которой может быть определена априори для каждого вида*узловых соединений. Таким образом, в оперативной памяти требуется хранить только те элементы, которые находятся в верхней части ленты. Они показаны на фиг. 1.4, е.

Третий этап состоит во включении в полную матрицу системы заданных граничных условий. Способ включения рассмотрен Б разд. 1.3.

Заключительный этап - решение полученной системы уравнений. Для решения могут быть использованы различные методы, некоторые из которых обсуждаются в гл. 20. Хотя вопрос решения уравнений и является чрезвычайно важным, он выходит, вообще говоря, за рамки этой книги.

Далее вычисляются напряжения, токн и другие выходные величины.

Любой расчет сетей осуществляется по намеченным этапам, которые должны быть хорошо поняты читателем. Хотя, безусловно, эти этапы важны для понимания метода конечных элементов, они, однако, не составляют его сути. Эти этапы хорощр

известны и обычно используются в строительной механике. Остальная часть книги посвящена йетоду приближенного представления сплошной среды эквивалентной системой конечных элементов. Если такое представление возможно, то описанная схема позволит осуществить расчет.

ЛИТЕРАТУРА

1. Tiraoshenko S. Р., Young D. Н., Theory of Structures, 2nd ed., McGraw-Hill

2. Livesley R. K., Matrix Methods in Structural Analysis, Pergamon Press, 1964

3. Przemieniecki J. . S., Theory of Matrix Structural Analysis, McGraw-Hill 1968

4. Martin H. C., Introduction to Matrix Methods pf Structural Analysis

5 jlnkins*w.M., Matrix and Digital Computer Methods in Structural Analy sis, McGraw-Hill, 1969. , ,

6. Turner M. J.. Clough R. W., Martin H С Topp L. J Stiffness and Defleo tion Analysis of Complex Structures, /. Aero. Scu, 23, 805-823 (1956),

7. Payne N. A., Irons В., частное сообщение, 1963.

ГЛАВА 2

КОНЕЧНЫЕ ЭЛЕМЕНТЫ УПР-УГОЙ СРЕДЫ. МЕТОД ПЕРЕМЕЩЕНИЙ

2.1. Введение

Часто для различных инженерных целей требуется знание распределения напряжений н деформаций в упругой сплошной среде. Тогда предметом исследования являются двумерные задачи о плоском напряженном и плоском деформированном состояниях, задачи об осесимметричных телах, об изгибе пластин и оболочек и наконец, исследование трехмерных твердых тел. Во всех случаях число связей между любым конечным элементом, ограниченным воображаемыми поверхностями, н соседними элементами бесконечно. Поэтому с первого взгляда трудно понять, каким образом такие задачи можно днскретизировать, как это было сделано в предыдущей главе для простейших конструкций. Эта трудность преодолевается следующим образом.

1. Сплошная среда разделяется воображаемыми линиями или поверхностями на некоторое количество конечных элементов.

2. Предполагается, что элементы связаны между собой в узловых точках, расположенных на их границах. Так же, как в обычных задачах строительной механики, основными неизвестными будут перемещения этих узловых точек.

3. Выбирается система функция, однозначно определяющая перемещения внутри каждого конечного элемента через перемещения узловых точек.

4. Функции перемещений однозначно определяют деформации внутри элемента через узловые перемещения. Эти деформации при известных начальных: деформациях и упругих свойствах элемента позволяют определить напряжения как внутри элемента, так н на его границах,

5. Определяется система сил, сосредоточенных в узлах и уравновешивающих напряжения на границе и некоторые распределенные нагрузки, а затем записывается соотношение для жесткостей в форме (1.3).

Далее могут быть использованы обычные методы решения зэдач строительной механики, описанные ранее. Очевидно, что такой подход является приближенным. Во-первых, не всегда легко добиться, чтобы выбранные функции перемещений удовлетворяли требованиям непрерывности перемещений между смежными элементами. В результате на границах элементов могут

нарушаться условия совместности (хотя в пределах каждого элемента эти условия, очевидно, удовлетворяются при однозначности функций перемещений). Во-вторых, сосредоточивая эквивалентные усилия в узлах, мы только в среднем удовлетворяем уравнениям равновесия. Обычно возникает локальное нарушение уравнений равновесия внутри элементов и на их границах.

Выбор формы элемента н функций перемещений для конкретных задач зависит от изобретательности и мастерства инженера, и совершенно ясно, что именно этим определяется точность приближенного решения.

Изложенный здесь подход известен как метод перемещений [1, 2]. До сих лор обоснование метода было нестрогим, хотя, в сущности, этот метод эквивалентен мнннмизацни полной потенциальной энергии системы, выраженной через поле перемещений. При подходящем выборе поля перемещений- решение должно сходиться к точному. Этот процесс эквивалентен хорошо известному методу Ритца, что будет показано в одном из последующих разделов этой главы. Там же будут рассмотрены необходимые критерии сходимости.

Эквивалентность метода конечных элементов процессу минимизации была замечена недавно [2, 3]. Однако еще Курант в 1943 г. [4] и Прагер н Синг в 1947 г. [5] предложили, по существу, идентичный метод. Более широкое обоснование метода позволит распространить его почти на все задачи, для которых возможна вариационная постановка. В этой книге будут рассмотрены некоторые такие задачи, не имеющие отношения к строительной механике.

2.2. Описание свойств конечного элемента

Правила получения характеристик конечного элемента сплошной среды, описанные ранее схематично, теперь будут изложены в более подробной математической форме.

Желательно получить результаты в общем виде, справедливом для любого случая. Однако чтобы облегчить понимание общих соотношений, они будут проиллюстрированы на очень простом примере плоского напряженного состояния тонкой пластины). В этом примере использованы элементы треугольной формы, показанные на фиг. 2.1. Соотношения общего характера напечатаны полужирным шрифтом, а выражения, соответствующие частному примеру, - нормальным. Как и ранее, используется матричная форма записи.-

) В действительности будет рассмотрено обобщенное плоское напряженное состояние. - ГГрим. ред.

2.2.1. Функция перемещений

Типичный конечный элемент е определяется узловыми точками 1 , /, m и т. д. и прямолинейными границами. Пусть пере-

Фиг. 2.1. Плоская область, разбитая на конечные элементы.

мещения любой точки внутри элемента задаются вектор-столбцом

{f} = [N]{6r = [N N N ...] б„ . (2.1)

где компоненты [N] являются в общем случае функциями положения, а {б} представляют собой перемещения узловых точек рассматриваемого элемента.

В случае плоского напряженного состояния вектор-столбец

содержит горизонтальное и вертикальное перемещения типичной точки внутри элемента, а столбец

содержит соответствующие перемещения узла i.

Функции Ni, Nj, Nm должны быть выбраны таким образом, чтобы при подстановке в (2,1) координат, узлов получались соответствующие узловые перемещения. Очевидно, что в общем случае

fi(xi, yi)=I (единичная матрица),

тогда как

Ni(x y,) = Ni(x, Уп) = 0 и т. д.,

что, в частности, достигается соответствующим выбором линейных относительно хну функций. Более подробно вопрос о выборе функций [Л^] будет рассмотрен в одной из последующих глав.

Функции [N] называются функциями формы. Онн, как будет видно из дальнейшего, играют важную роль в методе конечных элементов.

2.2.2. Деформации

Если известны перемещения во всех точках элемента, то в них можно также определить и деформации). Они находятся с помощью соотношения, которое в матричной форме может быть записано в виде

И = [В]{6Г: (2.2)

В случае плоского напряженного состояния представляют интерес деформации в плоскости, которые определяются через перемещения с помощью хорошо известных соотношений [6])

ди дх да ду

ди dv ду + дх

) Здесь под деформациями понимаются любые внутренние дисторсии, такие, например, как кривизна в плоской задаче.

°) Для того чтобы строки первого столбца образовывали ортогональный тензор, необходимо третью строку второго столбца умножить иа Vj. - Прим. ред.

[ 1 ] 2 3 4 ... 27