Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 2 3 [ 4 ] 5 6 7 ... 14

Р^Ро\/1-(ШУ-(ФУ,

где а н - соответственно большая и малая полуоси эллипса, то

у(х.У,2)= / (1- у1

So s

(2.52)

(2.53)

где So - наибольший корень уравнения третьей степени -±- + -L- + - = 1;

f - нормальная сила, действующая на область Поскольку

dw/dz - v;

э'и- bw dw -Т- (х, у, °°) = --(х, у, оо) = -(х, у, оо) = о,

по известному значению v производные от w, входящие в формулы (2.51), можно найти интегрированием:

~ -~-dz (а = 0,1,2).

г эх эу-

(2.54)

Таким образом, для вычисления напряжений достаточно найти одну функщ1ю \(х, у, z).

Так как подьштегральная функщм в (2.52) с учетом (2.53) обращается в нуль при S = So, то для производных от V верны следующие формулы:

э V 3Pz

эх 2 (fl+s ) V(6+ Эх

s (e+ s) 7(6+ s)s

av ЗР

2 (6 + s.) N/(a+s,)s.

(2.55)

(6 + s) V( + s)s

э'у 3 J

- /-

s, s V(F+l)(6~r7)

Производные от So определяем дифференщ1рованнем уравнения (2.53):

2х

2у

эх (e+So)r 8s, 2z

by (6 + s.)r

(2.56)

Y=Y(x,y.z) =

(fl+S,) (6+s.) s

Напряжение под центром контакта. На оси Oz координаты хиу равны нулю; при этом решением уравнения (2.53) является So = , а смешанные производные от v в (2.55) обращаются в нуль. Поэтому на оси Oz отсутствуют касательные напряжения, а а^, Оу и являются главными напряжениями. Из формул (2.55) следует, что

эу av

- -Z -

V(fl + z)(6 + z)

a из (2.51) с учетом P = 2тгроаЬ/3 az 1

(2.57)

где = z/b - безразмерная глубина; = b/a- отношение длин полуосей эллипса контакта.

Формула (2.57) получена В.М. Макушиным. Напряжение а^,на поверхности равное -ро, монотонно убывает по абсолютному значению, стремясь

к нулю при2-+оо.

в выражениях для и Оу входят норманьные эллиптические интегралы первого и второго рода

о \/1 - sin* ip

; Е(ф,е)= /Vl-esinVv.

(2.58)

О

где е = у/ I - - эксцентриситет эллипса контакта.

Для любого Sq верно проверяемое дифференцированием тождество

Отсюда следует

Эу 2np,z 1 nA7 , /

- =-[-(arcctg-, е) - V-

bz в а я s (fl + s )

£(arcctg-, е).

6 + s

(2.59)

Интеграи в формуле (2.55) для Э^у/Эх заменой s =actgv3 приводим к

2 ч/ л/Т7

--[£(arcctg-, е) - F(arcctg-, е)],

а'е' а д

э'у

-;-[arcctg-, е) - F(arcctg-, е)].

(2.60)

Интегрирование этого равенства по частям от z до < при Sq = z дает

Z г г

- [£(arcctg- ,е) - Fl(arcctg-, е)] + а а а

/б' + Z

+ 1- V-

а' + Z

В силу тождества

bva}ifdif

1 Е(ф,е}

= -те)]

(2.61)

(2.62)

Q(l-esinV)> е р' pVl-esin,

интеграл в формуле (2.55) для д'у/ду при s = actgvJ сводится к

1 1 \/ 7 \/ 7 -[-£(arcctg-, е) - F(arcctg-, е)] -

6 (a + s )(6 + s )

а с учетом Sq = z

э'у

-(arcctg-, е) -ее в

- /3*F(arcctg- , е)] -

V(fl+ z)(b + z)

(2.63)

Представив Э^у/Эд через левую часть (2.62) и проинтегрировав по частям от Z до °°, получаем

э'н- 2яр,

- [F(arcctg- , е) - j3F[arcctg-, е)] + е' а а

:гттгг

0 / a+z-

-- +-(V--1)

+ V(a* + r*)(b + z*) 6 + г'

По формулам (2.55), (2.60), (2.61) определяем

(2.64)

(1-2)+ {2р-рЫ---7 +

1+ Д'Г'+ Г'

+ - )F(arcctg(r), е) -(1 - j) F(arcctg03r), е)] а по формулам (2.55), (2.60), (2.63), (2.64)

(2.65)

р( 2и - 1) + 2т^р - 1) Е(атсат), е) + [2 - (1+ 2.)0]f+ 1- г.з'

+ (l-)F(arcctg(,e)] +

V(l+ ?)(!+

(2.66)

Выражения для и Оу можно привести к формулам, полученным В.М. Макушиным:

на поверхности (f = 0)

= 1 1,

2v+ &

о у 1+21-

Ро Ро 1+3

для цилиндров (Р = 0) 3-444

1+ д

= 2Kr-Vn);

(2.67)

= 2Г-

1+ 2Г'

Po s/1 + f

для круговой площадки контакта = 1)

1 + f

(2.68)

= - = - [(1 - XI - Г arcctgr)------------

Ро 2(1 + f)

Для получения этих формул нз (2.65), (2.66) необходимо раскрыть неопределенность при е 0. Все напряжения стремятся к нулю при f >.

Напряжения в плоскости Oyz. Наибольший интерес представляет распределение напряжений в плоскости, проходящей через малую ось эллипса контакта перпендикулярно к поверхности. При качении шарика по желобу в направлении Ох каждая частица материала шарика или кольца испытывает цикл переменного нагружения. Согласно Лундбергу и Пальмгрену, на поверхности, т.е. при X = О, для удобства выкладок вводим углы у и р, связанные с декартовыми координатамиz следующими равенствами:

(2.69)

у =\/Ь^ + atg7sinv5; z = atg7cosi. Тогда решением уравнения (2.53) является

So=atg4. (2.70)

Кривые 7 = const представляют собой части эллипсов с центром в точке О и полуосями V fc +atg7 и а tgy (рис. 2.10), кривые const-гиперболы с асимптотамид = zig, проходящие через точкиг = 0,у = Ь sin( = 0,2).

Из формул (2.55) следует, что прих = О равны нулю Э'у/ЭхЭд и 8v/3x8z и, следовательно, Тху = tz = С Согласно (2.51), (2.55), (2.56), (2.70),

Тут cossinsinT

- = -/3-

Ро tgT + 0cosV

(2.71)

Напряжение Tyz = О при у = 0(р = 0), при z = О (у? == ± 7г/2 или 7 = 0), при у' + г' оо (7 7г/2). Наибольшее значение ]ту2 \ определяем с помощью уравнений bTyzlbp = dTyz/by = О, котортле сводятся к системе 66

ср=-73

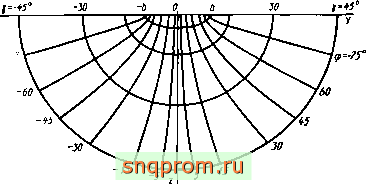
Рис 2.10

tg7(2tgV + tgV-1) =/3;

tg7(l+tgV)(2tg4+ 1) = ;

откуда tg7 = tgv? - 1 = ? - 1, где t - решение уравнения (? - 1)(2г - 1) = = j3. Значение t как функции j3 с точностью ± 2 % представим, согласно Б. Хэмроку и Д. Даусону, формулой

f = 1+ 0,3044 .

Координаты точки MaKCHM3Tvia \ту2 \ находим по формулам

2о=ГоЬ = №+ 1)ч/2Г^] =flV(?-i)/(r + i);

Уо = ±nofc = ± ьЫф+ i)K2t- mt + 1).

Максимум I Tyz\ есть

To=Poy/2r~T/l2tit+ 1)].

(2.72)

(2.73)

(2.74)

Напряжения а^, Оу, Oz определить несколько сложнее. Формулы (2.59) и (2.60) верны для любых х, у, z. Подстановка в них Sq из (2.70) дает

3v COST /, - = - 27фоГ[-+ tg7 - £(- - У, е)];

9Z tgT 2

(2.75)

[£ (- -7.e)-F(- - у,е)].

Эх ее ~ 2 2

В выражении (2.55) дляЭ'у/Эд появляется отличное от нуля слагаемое,

содержащее dso/dy. Подстановка (2.69) и (2.70) с учетом (2.63) в (2.55) и следующей из (2.69) зависимости z от 7 и j приводит к результату

э'у ЗР

(tgT+ 0) sin7 (tgT + 0) -

- ~ {E{.~ - 7, e) - F( - 7, e) ],

где 17 =/6.

Согласно (2.51), (2.55) и (2.70),

Oz 0cos7(tg4+0

(tg7+/3)-0T,

(2.76)

(2.77)

Видно, что прн 17 = о это выражение совпадает с (2.57). а при \у\> b и Z = 0(vJ = ± 7г/ 2) напряжение 5 = 0. В соответствии с (2.54), интегрирование равенства (2.75) дает

щдЛ- , е) -F( , е)] + 1 - Г-

[arctg-- arctg-]; Vl-(e + /3 n )cos7.

e 3t) /Зг)

(2.78)

Из (2.51), (2.75), (2.78) следует

eY е

)3(1 - 2i)[l + У--(arctg-- arctg-)] +

е pri 3т)

cos 7 ,-.-, п

+ 2К1 -)f-- Vt?7+1+ 2Г№ - и)Е(- - У.е)-

tg7 2

- f)F(--у,е)].

(2.79)

При = О эта формула совпадает с (2.65), а на малой оси Эллипса контакта, т.е. при 7 = О = 0,Ы < 1),

= - -[(1 - 2р)+ (2v- /3)Vr-

.-(arctg--arctg-)],

(2.80)

при 7? = ± 1, Т.е. на концах малой оси,

= -(1-2) (1--arctg-).

Интегрирование выражения (2.76) в соответствии с (2.54) дает

(2.81)

Э'к 2яр„

COS7Sln7

- Е(--7. е) +

V1 -ecos 7 0т, е

+ F(- г е)] +-[arctg- - arctg(- \/sin7+13(1 -t?)cos4)]+

Vsin7 + 0(1 - Ti)cos7

+ j3(--1) .

sin 7 + P cos 7 Из (2.51),(276), (2.82) и (2.75) следует

(2.82)

+ 2v - +

1 - 21-

+ т - 2f)

tg7 Vtg7+ P

Дт) e e

]sin7 +

[arctg--arctg(-Vsm7 + jSl - r?)cos7l +-

N/sin7+ 0(1 - Ti)cos7 , я

+ V-y P i--T 2r[(p-l)F(- -7.e) +

sin 7 + p cos7 2

+ (1 - )PF(- - 7, e)

При = 0, tg7 = z/a эта формула сводится к (2.66); при этом на малой оси эллипса контакта

(2.83)

= --[р(2р - 1) + (1 - 2pei)s/r +

Р'(1 - 2v)n

(arctg--arctg-

(2.84)

на концах малой оси

-=-(1 - 2v) - (-arctg--1).

Ро е' е Р

(2.85) 69

Формулы (2.77), (2.79) и (2.83) можно также записать в переменных V> и 7, выразив г? и f через <риус учетом соотношений (2.69).

Линейный контакт. Эллипс контакта в подшипниках качения, как правило, достаточно вытянут ( = 0,1...0,3), поэтому представляют интерес формулы для напряжений при 3 С 1. Для роликового подшипника j3 = 0. При - О координаты (2.69) неудобны, так как а °°. Используем переменные 17,5 и X = so/b; тогда при j3 = О

Tyz

(2.86)

При необходимости учесть следующий порядок в разложении Ту и Oz по степеням j3 выражения (2.86) следует умножить на 1 - Х/3/2. Тогда они будут верны на расстояниях от центра контакта, много меньших длины большой оси эллипса. По формулам (2.79) и (2.83) с учетом связи 4y = Vsola

- =-2Г(\ Ро

/l+ \

:(V-

/l + \ X

(2.87)

в переменных ip,a = s/J/b - s/Y

У

a co% If

(2.88)

= -cosvJ[(-

+ cos

+ l)Va + 1 - 2a].

Одним из главных напряжений является Ох- Два других определяем по формулам

= - cosVa + 1- aXl ± ). (2.89)

Ро s/ot + cos

Максимальное по всем возможным ортогональным к плоскости Oyz площадкам касательное напряжение

тах (а VaMT-a)cosv>

\Jcosifi

(2.90)

Условия экстремума Tmax(9Tmax/9v5 = Эттах/Эх = 0) приводят к равенствам \р = О, а V + 1 = 1. Корень последнего уравнения а 0,786. Таким образом, максимальное по осям Оу и Oz значение Ттах = 0.3 ро достигается на глубине z = 0,786 b. На оси Oz главные напряжения Oi и совпадают с я Оу, так что площадки, на которых касательное напряжение максимально, делят углы между осями Оу и Oz пополам.

С точки зрения наблюдателя, связанного с точкой или линией контакта, при качении шарика или ролика частицы материала проходят через поле напряжений, испытывая цикл нагружения. При фиксированном значении Z имеем z/cos <р,а = f/cos tfi. Формулы (2.88) при заданном f прини-

мают вид

Tyz ?cos sin¥

f + COSV

Oz . Vf + cos*

-- = - cosV--

Po f + cosV

Z =2г--vr + cosv:

(2.91)

f + cos*

Видно, что в процессе движения частшц>1, т.е. при изменении р, напряжение Ту меняет знак, а и а^, остаются сжимающими. На площадке, наклоненной под углом к плоскости Оху (рис. 2.11), действует касательное напряжение

Тф =-T,zCos2i -0,5(о у - az)sin2i .

С учетом формул (2.91)

cosVsinvcos2 - lcos?v> - ?(ч/{- cosV- ))sin2(<

(2.92)

Для = ± 7г/2 при всех \& напряжение равно нулю. Другие значения ур, при которых обращается в нуль, определяем иэ условия

cos ifimtfi

= tg2\(/.

(2.93)

cosV - f(Vf + cosV - ?)

Корни ? = cosv знаменателя можно найти из уравнения t* -{1 - 20f. Прн f 1 Г = 0,5, (/) =±0,57. Для больших f условие (2.93) имеет вид

Щ2ф = tg2v>.

Таким образом, для любого ф Ф О напряжение обращается в нуль два раза на интервале (- 7г/2, я/2), а для = О - один раз. Достаточно

Рис. 2.11

г 3 и

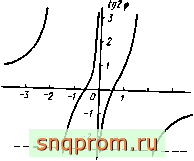
Рис. 2.12

ем из (2.91); приф = п/8 Р и напряжение -- Ту определя-

V8 = COsVsiny. - cosy + + cose,- f)

(f + cosV)\/2

при ф = Ti/4

Ч* f(VP+HiV- f) - cosV Po f + cosV

при Ф = 37Г/8

cosisin;* cosv - ?(\/? + cos-r f)

Po (f + CO 5*)71

Условие дтф/д^р = О зкстремума т,;, прн фиксированном f имеет вид cos2i [cos(/3(cosi/)+ 4f*cosi/>-3?)] + f sin

-Г3гг.в ,л+ /<?-2-2 . vi.-. - (2.94)

Г(ч/ГГ4Г'- 2Г); п 94) приводим к виду

Отсюда при ф = 0 cosV = Г(\/3 + , , ,

= f(v/3T4f*- 2f)/3. Условие (2.911.5 ...: Р = / cosV =

tg2 =

где

3u - 1

(3 -

(2.95)

График функции (2.95) представлен на рис. 2.12. Значения и, при которых \тф I максимально, определяются как абсциссы точек пересечения графика штриховой линией. Например, для ф = я/8 корни уравнения (2.95): и= 1; - 2 ± ТТПри и = м, = 1. tgV=\/l причем i, я/4,

если f < ; прн ы = з = ~ 2 ±

(3 + 2V3)? + ч/(7 T4vTy(7f +4)-tgV2,3 =--

Если f -> оо, то 12 - 19°, vs - 70°. Для i/ = Зя/8 углы vl, va, меняют знаки по сравнению с случаем ф= Зя/8. В общем случае углы определяем из формулы

tgV = o,5[ - 1 + VPo7T17Tl/f],

причем знак tgi,;? совпадает со знаком и. На рис 2.13, а-д изображены зави-

0,3-.5 В

Рис. 2.13

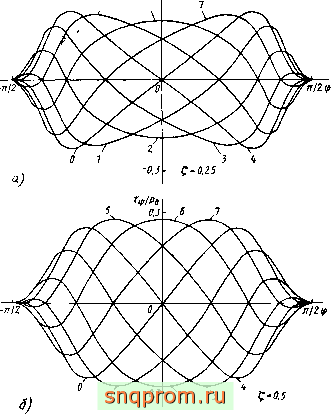
самости от для различных значений i и f. Кривые 0-7 соответствуют значениям ф от нуля до 77г/8 с шагом 7г/8.

касательное нагружение. Пусть на границе полупространства касательная нагрузка Тх{х, у) направлена вдоль оси Ох и распределена по области Напряжения в упругом полупространстве определяем по формуламМ.В. Ко-ровчинского:

ах = -[2(1+ - 2я Эх

Э' Э'и

- (1 - 2p)z-

aw э'и - 2v-]:

э'у

2я ЭхЭг 1 Эу

2я Эд

[--(1-2)г-

- 2v-

эхэ>-

(2.96)

Txz =

1 Эу

-(--z-

2-п Эг

Z Э'у

Tyz=--

2я ЭхЭд

где V И w даются формулами (2.51) с заменой р на Тх и, кроме того, введен потенциал

и(х, у, z) = Ят-хЙ, vyddn; а

г= /ik~xf + (rj-yf + z\ (2.97)

Если касательная нагрузка распределена согласно теории Герца, т.е. тх(х. У) = T%s/l-(x/af -{ylbf (г° - максимальное значение напряжения в зоне контакта),то

v(x, у, z) = /(1----4 . e+s

--- , - (2.98)

)+ S S V(e+s)(b+s)s

где - касательная сила, действующая на эллиптическую область контакта.

Тх = 2пт°хаЬ/3.

(2.99)

По известной функции \(х, у, z) можно определить производные от w/и и, входящие в формулы (2.96), с учетом следующих соотношений:

=- f

3 3v

2 Ьх°ду

-dz (а = 0,1, 2,3);

(2./00)

а'м Эу Э'у -= 2- + X-

ЭхЬу Ъу Э'и

Э'у

(2.101)

Эу Э'у

Итак, для определения компонент тензора напряжений достаточно найти соответствующие производные от v. Для них, дифференцируя выражение (2.98), получаем следующие формулы:

э'у ЗГу

2 (a + s ) V(6*+s )s * Эх

(2.102)

2 S s V(fl+s)(6 + s)

Интегралы в формулах (2.102) можно выразить через нормальные эллиптические интегралы Лежандра первого и второго рода (2.58). Тогда приs = actgifiHb/a получим

/-г-- =-[F(arcctg-, е) -(arcctg-е)];

J (e + s) V(6 + s)s e

/ - .

- F(arcctg

2 1 чЛТ^ , = -~ [-E(arcctg-, e) -

0 (1 + S /fl)(P+ So/fl)

(2.103)

Рис. 2.14

i V(fl + s)(6 + s)

£(arcctg-, e)].

Определим компоненты тензора напряжений в наиболее важных частных случаях. Предварительно введем безразмерные переменные

(2.104)

Напряжения под центром контакта. На оси Oz х = у = О, поэтому Sq -= или в безразмерных переменных

Из (2.102) и (2.103), с учетом (2.105), имеем ЗГх

(2.105)

Э'у

а'0 ЗГх

1 + 0f

r£(arcctgr, е)]; [F(arcctg3r, е) - (arcctg/ЗГ, е)];

(2.106)

остальные производные, входящие в (2.96), равны нулю. Найдем компоненты тензора напряжений (рис. 2.14) :

Ох = Оу= °z = тху = Tyi = 0;

Ч

1+0?

-F(arcctgr, е)].

[(2--)E(arcctgr,e)-е' 0

(2.107)

Предельным переходом при 3 О найдем из (2.107) выражение для компоненты tz тензора напряжений в контакте цилиндров:

х

(2.108)

что совпадает с аналогичным выражением, полученным М.М. Савериным.

Для кругового контакта 0 в ряд по степеням е, получим

1 = !+£. (3arcctgf - --т% -2 1+ f

1. Разложив эллиптические интегралы ) (2.l/)9)

Напряжение в плоскости Oyz. В плоскости Oyz х = О, поэтому уравнение (2.53) для определения Xq упрощается и сводится к квадратнрму. Для простоты вычислений введем координаты ан ip, изменяющиеся Соответственно от О.до оо и от -7г/2 до +7г/2, связанные с декартовыми координатами следующими зависимостями: I

у = fcchasini, z = feshacosj. (2.110)

Координата о; связана с введенной ранее координатой 7 соотношением

tg7 = 3sha, (2.111)

поэтому координатные кривые а и имеют тот же вид (см. рис. 2.10). Координаты а и tp использованы М.М. Савериным при исследовании контакта цилиндров, что позволит нам без лишних сложностей рассматривать предельные переходы к решению задачи о контакте цилиндров. Координата 7 удобна лишь при рассмотрении кругового контакта, а также в качестве аргумента в эллиптических интегралах. Решая уравнение (2.53), получаем

So=fcsha, (2.112)

или, с учетом соотношения (2.111),

So=fltg7. (2.113)

откуда следует, что в эллиптических интегралах (2.103) первый аргумент - угол arcctg л/ (So/a ) = тг/2 -7.

Определим компоненту tz тензора напряжений в плоскости Oyz, учитывая, что 5 = 5 = 5z = Tyz = 0. Из (2.102) и (2.103), с учетом замен (2.110) и (2.113),получим

ЗТхСОЪ cha тг

-[---£ (-7,e)sha];

а'З Vl + 0sha 2

ЗТх

(2.114)

а'е' 2 2

Подставив (2.114) в формулу (2.96) для Txz и учтя выражение (2.99) для Тх, найдем (рис. 2.15,а; = 0,5)

Txz cha

= - cosyv

V 1 + 0 + sh а

3 sha

+ [(2-

1 я

--)£ (- -у,ё)-0 2

-F(-

(2.115)

Рис. 2.15

Предельным переходом прн Р -* О получим иэ (2.115) выражение для Txz в контакте цилиндров (рис. 2.15, б): 13=0:

- = -ехр (-a)cosv?, (2.116)

(15 I

г

	т
	/ к 1 /л
0,5 1,0 I)

		/ 1

что совпадает с выражением, полученным МА1. Савериным,

При j3 1 получаем формулу для т^ Р круговом контакте (рис. 2.15, в):

= -cos¥ [l - 1,5 (--7)tgr+ 0,5 sin*7].

(2.117)

Напряжения в плоскости Oxz. В плоскости Oxz j = 0. Аналогично предьщущему введем координаты е ифс помощью формул

х = achesini , z = ashecosi/.

Тогда наибольший положительный корень уравнения (2.53)

о =ash€ или, после замены tg7 = she,

So=a*tg7.

(2.118)

(2.119)

(2.120) 79

Рис. 2.16

Определим компоненты тензора напряжений. В плоскости Oxz - yz = 0. Определим компоненту Txz- Для этого найдем 9v/3z и bf/dx, используя формулы (2.56), (2.102), (2.103) и учитывая (2.118)-(2 120) :

Э'у ЗТх

3TxCOs4i \/0+ she п

2 2 t----- T,e)she];

che thesini)/

1 (2.121)

,---[Fi--7. е) -

V+ she(she + cosi(() e 2

Подставляя (2.121) в формулу (2.96) для г^г и учитывая (2.99), получаем (рис. 2.16)

1 1 1Т 1 я

thesin ф

1 ч 3+ she

+--+ -

0 sheche V+ sheCshе + cosi )

Для контакта цилиндров (при /3 О, = 0)

(2.122)

что уже было получено ранее [ см. (2.108)]. Для кругового контакта (при

= -cos\t[l +

sinsin п

--1,5 (-- - 7)tg7 +

cos + tg 7

+ 0,5sin7].

(2.123)

Определим компоненту a. Для этого получим d\/dxdz из (2.102) и (2.56) подстановкой в них формул (2.118) и (2.119) :

f)xiz в' Vr+she(she + сое'!/-)

Тодставив (2.124) и (2.99) в формулу (2.96), получим

(Jshesini cos ф

(2.124)

А V(3 + she(she+ cosф )

ОгсюА предельным переходом при /3 -* О получим, что для контакта цилиндров = О, а при (31, для кругового контакта,

62 \ sinisini/zcosi/( Тх Г у^ cosi/-

Определение компонент Ох, Оу и Тху тензора напряжений, имеющих в своем составе, согласно (2.96), производные от w, - задача более сложная.

В плоскости Oyz Ох =Оу = 0. Для определения Тху необходимо знать выражения ддя dw/dxby. Из (2.100). (2.102), (2.56) и (2.104) имеем

ЗхЬу (1+ psh{) (cht- г,)

После замены под знаком интеграла переменной на по формуле

1 А'п' + е'? ch=-V-

1-г' получим в переменных avi

ЭхЭу в'е'(е' + ;3chc<sin(p) е' + pchasinip

- 1+-

echasin Pchacosip

- ( arctg

/Jchasin

- arcctg-

tgs/e + 0 cha

>/e + psha Для остальных производных имеем Эу

э'и

ду ЭхЭу

ethc

д' ,/1 +psh а

iL -[- Д--7,.)Д--7..)

1 2 3 [ 4 ] 5 6 7 ... 14